Quantum classical correspondence :
Classically chaotic systems display sensitive dependence on initial conditions. Many physical systems such as the driven and damped pendulum, atoms in strong magnetic fields, nonlinearly coupled oscillators and periodically driven rotors exhibit this property. Chaos, of course, pervades anything from weather to perhaps even stock market dynamics. See my somewhat non-technical talk on Hamiltonian chaos for more details.The quantum dynamics of such systems do not display dependence on initial conditions. One recurring theme of my research is to explore and understand the manifestations of classical chaos in the quantum dynamics. In particular, interest is foucussed on how the rich variety in classical dynamical structures affect the quantum spectra. Recently, we had studied quantum-classical correspondence in a non-KAM system.
Chaos, quantum localisation and interactions :
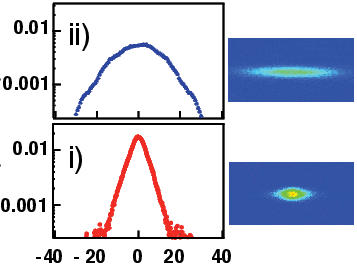
The interplay between chaotic dynamics, localisation and interactions is of special interest especially in the context of driven quantum systems. Kicked rotor, a pendulum periodically kicked by an external potential, is a prominent and well studied chaotic system We study different variants of kicked rotor that throw light on the connections between the quantum dynamical localization, a variant of the Anderson localization, and classical (sub-)diffusion. We recently wrote a detailed review article on Quantum kicked rotor and its variants: Chaos, localization and beyond in Physics Reports (2022).In a recent work that combines theory, numerics and cold atoms experiment (in collaboration with my colleague Umakant Rapol), we have shown how specific manipulation of kick sequence imparted to a rotor can lead to control of quantum decoherence, which shows up as a decay of localization.
In general, the role of interactions and how they affect localization properties in chaotic and many-body systems is explored. The physical systems of interest range from coupled kicked rotors and kicked tops to quantum spin-chains.
Random matrix spectra :
Random matrix theory (RMT) is widely used in physics (in condensed matter physics, nuclear physics etc.) to understand the spectral signatures of complex quantum systems and as a qualitative indicator of underlying classical dynamics. RMT is extensively applied in the study of chaotic quantum systems. Recently, we had obtained a series of results for the higher order spacing ratio distributions in random matrix theory and complex quantum systems.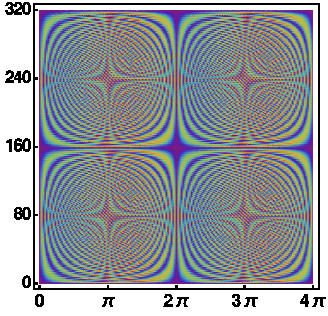
Quantum computing and machine learning :
Quantum computer is expected to speed-up certain class of problems, the prime factorisation being one such example. One of the central resource for a quantum computer is the quantum entanglement. Our research is focussed on studying entanglement (and more generally quantum correlations) properties, and curiously, to understand how it is affected by classical dynamics in the case of chaotic and many-body systems. Our recent representative paper on this topic is Phys. Rev. E 95, 012216 (2017).Another exciting area of interest we are starting on is the quantum machine learning (QML). Many machine learning tasks can possibly benefit from their quantised versions. With the advent of real quantum computers, we might actually be able to implement QML algorithms in some years. This has both fundamental and practical benefits, as discussed in Nature 549, 195 (2017).
Complex Networks :
has emerged as a unified framework to study many complex systems, ranging from stock markets to biological processes. We are mainly interested in the dynamical processes on networks, their properties and the interplay between network structure and dynamics on networks. The dynamical processes that we study can range from random walks to coupled chaotic systems. These are relevant for many transport processes on networks and also for such applications as web search engines and online recommender systems.
Extreme events :
Extreme events are an interesting emergent phenomena in complex systems. Floods, droughts, traffic jams, mobile congestion are some of the commonly encountered extreme events. Unlike floods and droughts, the latter two are examples of extreme events taking place on networks. The aim is to not only understand the properties of extreme events on networks but also explore the possibility of controllinng them. Our earlier research in the context of random walks on networks has showed a rather counter-intuitive property that extreme events are more likely to take place on small degree nodes of a network than on hubs. Our first paper on this topic is Phys. Rev. Lett. 106, 186701 (2011). I co-edited a special issue on Extreme events and its applications and its introduction provides a brief overview of the subject.